Todo lo que necesitas saber sobre los Números Racionales (Q)
¿Qué son los números racionales?
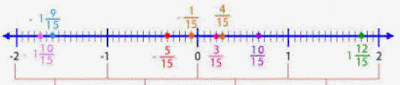
Representación de números racionales
Los números racionales pueden
representarse de varias formas. Además de la forma de fracción y decimal,
también pueden mostrarse en una recta numérica. En la recta numérica, los
números racionales se ubican entre los números enteros, y cada número racional
tiene un lugar único en la recta en relación con los demás números racionales y
enteros.
Operaciones con números racionales
Las operaciones básicas con números racionales son
similares a las operaciones con fracciones. Para sumar o restar números
racionales, es necesario tener un denominador común. Para multiplicarlos,
simplemente se multiplican los numeradores y los denominadores entre sí. Para
dividirlos, se multiplican en cruz los numeradores y denominadores. Es
importante simplificar las fracciones resultantes siempre que sea posible.
Suma de números racionales:
Ejemplo1:
Para sumar estas fracciones, primero necesitamos tener un denominador común. En este caso, el denominador común es 4. Entonces, convertimos las fracciones para que tengan el mismo denominador:
Ejemplo 2:
Resta de números racionales:
Para restar estas fracciones, primero necesitamos tener un denominador común. En este caso, el denominador común es 6. Entonces, convertimos las fracciones para que tengan el mismo denominador:
Ejemplo:
División de números racionales:
Ejemplo:
Para dividir estas fracciones, multiplicamos la primera fracción por el inverso de la segunda fracción
Propiedades de los números racionales
Para el conjunto de los números racionales con las operaciones de suma y
producto
Conmutativa:
Ejemplo:
Distributiva:
Ejemplo:
Propiedad de identidad o neutro:
Existe un número racional, conocido como el elemento
identidad, que no cambia ningún número cuando se suma o multiplica por él. Este
número es 0 para la suma y 1 para la multiplicación.
Propiedad de simetría:
Elemento simétrico respecto de la suma para cualquier número racional
es , llamado elemento opuesto, puesto que + =0
Lo mismo ocurre en el caso del elemento simétrico respecto del producto, para todo número racional q =, distinto de 0, existe = , llamado inverso multiplicativo tal que * = =1
Aplicaciones de los números racionalesLos números racionales tienen aplicaciones en una amplia variedad de campos, incluyendo la física, la ingeniería, las finanzas y la informática. En la física, por ejemplo, los números racionales se utilizan para representar mediciones precisas, como las fracciones de una cantidad total. En la ingeniería, los números racionales son esenciales para calcular medidas exactas y diseñar estructuras eficientes.
En resumen, los números racionales son una parte esencial de las matemáticas que tienen una amplia variedad de aplicaciones en la vida cotidiana y en numerosos campos profesionales. Entender cómo trabajar con números racionales es fundamental para desarrollar habilidades matemáticas sólidas y resolver una variedad de problemas numéricos.
Mayor información:
descarga